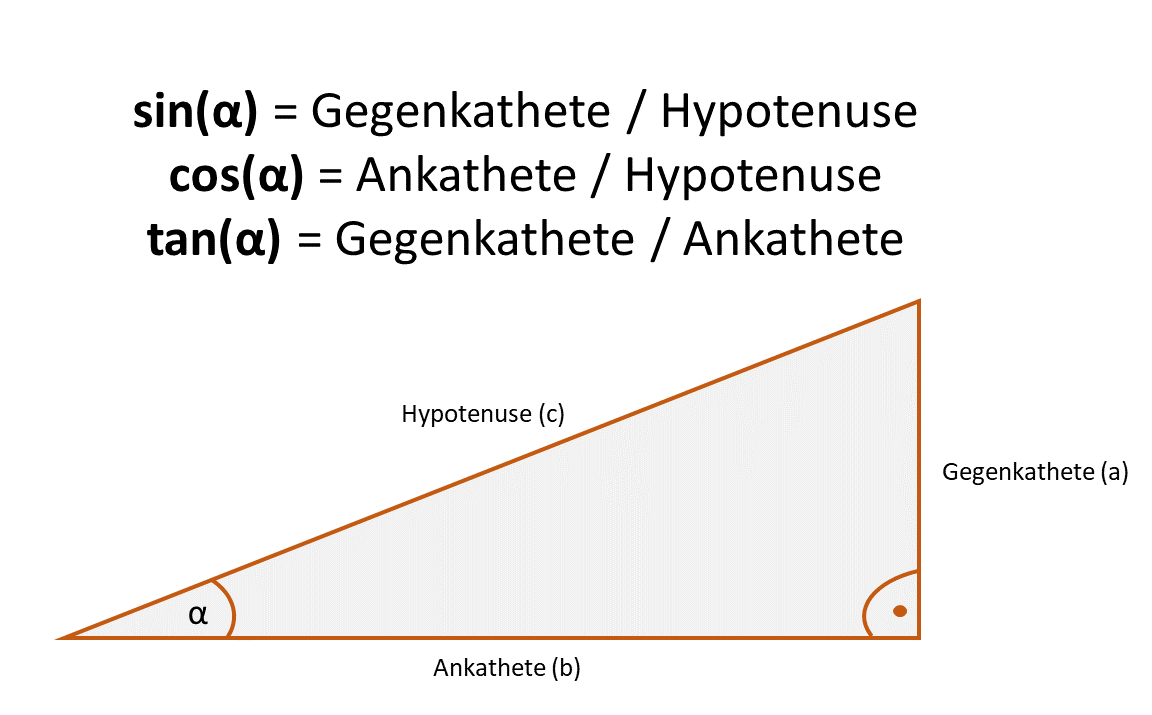
Tangens-Formel:
tan(α) = Gegenkathete / Ankathete
Sinus-Formel:
sin(α) = Gegenkathete / Hypotenuse
Cosinus-Formel:
cos(α) = Ankathete / Hypotenuse
Trigonometrische Funktionen zur Winkelberechnung
Je nachdem, welche Längen im Dreieck bekannt sind, ist entweder die Formel für den Sinus, den Cosinus oder den Tangens anzuwenden.
Tangens (tan) - Tangenssatz
Der Tangens (tan) wird über die Gegenkathete geteilt durch die Ankathete berechnet.
tan(α) = Gegenkathete / Ankathete
Beispiel:
Beginnen wir mit dem Tangens an einem Beispiel. Nehmen wir an, unser Auge bildet mit dem Boden eine Einheit und wir blicken aus einer Entfernung von 100 Metern auf die Spitze des Kölner Doms. Die Höhe des Kölner Doms ist bekannt und beträgt 157,38 Meter. Wir fragen uns, unter welchem Winkel nun die Spitze des Kölner Doms gesehen wird?
Die Antwort lässt sich bereits aus den vorliegenden Daten unter Zuhilfenahme der Tangenswinkelfunktion berechnen. Der Tangens berechnet sich aus der Gegenkathete (Höhe des Kölner Doms) geteilt durch die Ankathete (Entfernung zum Kölner Dom), also 157,38 Meter geteilt durch 100 Meter. Das Ergebnis (1,5738) ist eine dimensionslose Zahl und wird in den Taschenrechner eingegeben. Danach zuerst auf die "Shift" oder "Pfeil nach oben Taste" Taste drücken und dann auf die Tangensfunktion (tan).
Das Ergebnis zeigt dann die auf zwei Stellen hinter dem Komma gerundete Zahl von 57,57. Und das ist bereits der Winkel, unter dem wir in unserem Beispiel bereits den Kölner Dom sehen können, also unter einem Winkel von 57,57 Grad.
Sinus (sin) - Sinussatz
Der Sinus (sin) wird über die Gegenkathete geteilt durch die Hypotenuse berechnet.
sin(α) = Gegenkathete / Hypotenuse
Beispiel:
Gehen wir nun über zur Sinusfunktion, die sich mit einem analogen Vorgehen berechnen lässt. Nur sind uns in diesem rechtwinkligen Dreieck zwar die Höhe des Kölner Doms bekannt, aber nicht die direkte Entfernung zum Kölner Dom auf dem Boden, sondern die direkte Entfernung zwischen Auge und Spitze des Kölner Doms. Diese wird in dem hier skizzierten rechtwinkligen Dreieck auch als Hypotenuse bezeichnet. Berechnen wir abermals den Winkel aus der Höhe des Kölner Doms und der Hypotenuse von 186,37 Metern.
Der Wert der Hypotenuse wurde so berechnet, dass er wieder einer Entfernung zum Kölner Dom von 100 Metern entspricht. Wenn also nun nur die Länge der Strecke zwischen Auge und Spitze des Kölner Doms (Hypotenuse) und die Höhe des Kölner Doms bekannt wäre, und wir wieder nach dem Winkel fragen, kommt nun also der Sinus zum Einsatz. Die Winkelformel für den Sinus berechnet sich aus der Höhe des Kölner Doms geteilt durch die Entfernung zwischen Auge und Spitze des Kölner Doms in unserem Beispiel. Also 157,38 Meter geteilt durch 186,37 Meter.
Die dimensionslose Zahl von gerundet 0,84 wird abermals in den Taschenrechner eingegeben, die "Shift" oder "Pfeil nach oben Taste" gedrückt gefolgt von der Taste "sin" und das Ergebnis ist wieder der uns bereits bekannte Winkel von rund 57,6 Grad.
Cosinus (cos) - Kosinussatz
Der Kosinus (cos) wird über die Ankathete geteilt durch die Hypotenuse berechnet.
cos(α) = Ankathete/ Hypotenuse
Beispiel:
Der Cosinus benötigt in unserem Beispiel die Entfernung zum Kölner Dom von 100 Metern (Ankathete) geteilt durch die bereits bekannte Hypotenuse (186,37 Meter). Diesmal ergibt sich durch Division von 100 Metern geteilt durch 186,37 Meter die dimensionslose Zahl von 0,537. Eingetippt in den Taschenrechner und wieder die "Shift" Taste bemüht, ergibt bei Anwendung der Taste "Cos" (für Cosinus) den Winkel von rund 57,6 Grad.