Skizze
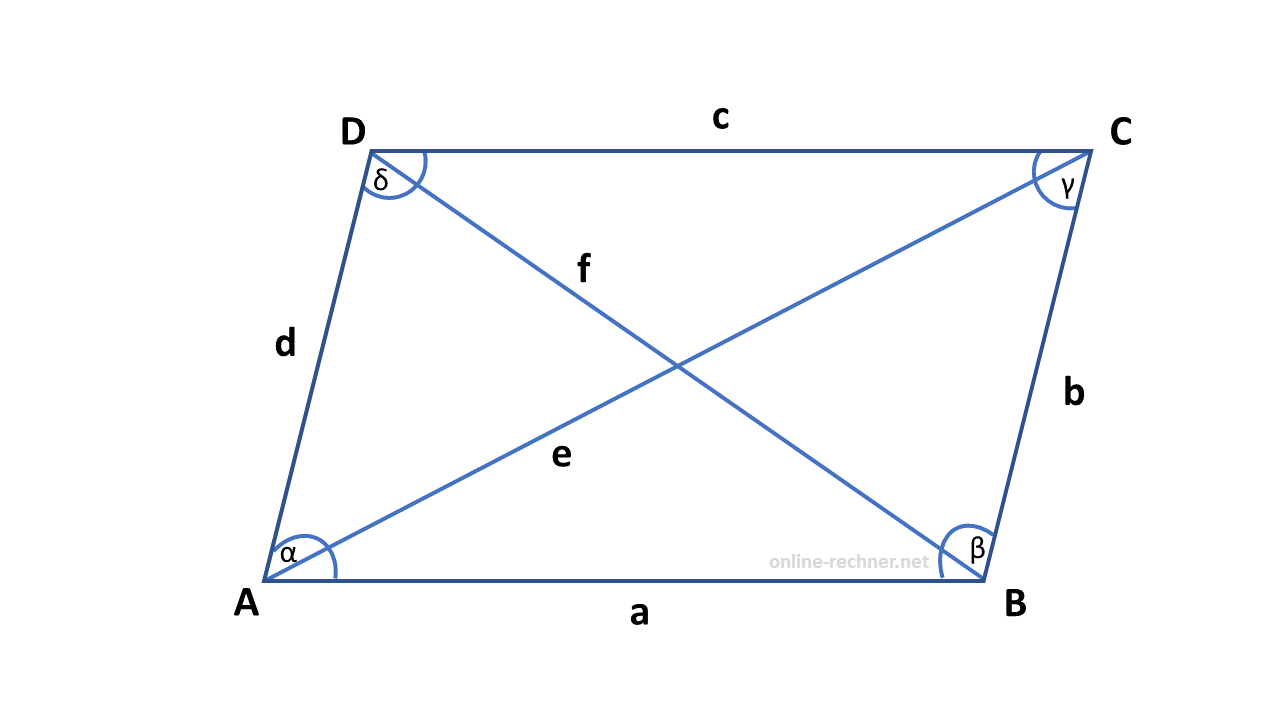
Flächeninhalt eines Parallelogramms
Formel: a * ha = A bzw. b * hb = A
Beispiel-Rechnung: 5cm * 6cm = 30cm2
Umfang eines Parallelogramms
Formel: 2a + 2b = U (Umfang)
Beispiel-Rechnung: (4cm * 2) + (3cm * 2) = 12cm
Ein Parallelogramm ist eine spezielle Art von Viereck, bei dem gegenüberliegende Seiten parallel und gleich lang sind. Es gibt verschiedene Eigenschaften und Messungen, die man bei einem Parallelogramm berechnen kann, einschließlich Fläche, Umfang und die Längen der Diagonalen.
1. Flächenberechnung: Die Fläche eines Parallelogramms berechnet sich aus dem Produkt der Basis (b) und der zugehörigen Höhe (h). Die Formel lautet: A = b * h. Die Höhe ist dabei der senkrechte Abstand zwischen den Basen.
2. Umfangsberechnung: Der Umfang eines Parallelogramms ist einfach die Summe aller vier Seiten. Da in einem Parallelogramm die gegenüberliegenden Seiten gleich lang sind, kann der Umfang auch berechnet werden, indem man die Länge der Basis (b) und die Länge der Seite (a) verdoppelt: U = 2*a + 2*b.
3. Diagonalenberechnung: Die Längen der Diagonalen in einem Parallelogramm können mit Hilfe des Satzes des Pythagoras und der Winkel zwischen den Diagonalen berechnet werden. Die Formel lautet: d² = a² + b² - 2ab*cos(Θ), wobei a und b die Seitenlängen und Θ der Winkel zwischen den Seiten ist.
Diese Berechnungen sind grundlegend für das Verständnis der Eigenschaften eines Parallelogramms und sind ein zentraler Bestandteil vieler Probleme in der Geometrie und der technischen Anwendung.
