Flächeninhalt eines Rechtecks
Formel: a * b = A (Fläche)
Beispiel-Rechnung: 10cm * 3cm = 30cm2
Flächeninhalt eines Quadrats
Formel: a * a = A (Fläche)
Beispiel-Rechnung: 5cm * 5cm = 25cm2
Flächeninhaltninhalt eines Dreiecks
Formel: (a * h) / 2 = A (Fläche)
Beispiel-Rechnung: (3cm * 5cm) / 2 = 7,5cm2
Flächeninhalt eines Trapez
Formel: ((a + c) * h) / 2 = A (Fläche)
Beispiel-Rechnung: ((5cm + 3cm) * 7cm) / 2 = 28cm2
Flächeninhalt eines Parallelogramms
Formel: a * ha = b * hb = A (Fläche)
Beispiel-Rechnung: 5cm * 7cm = 35cm2
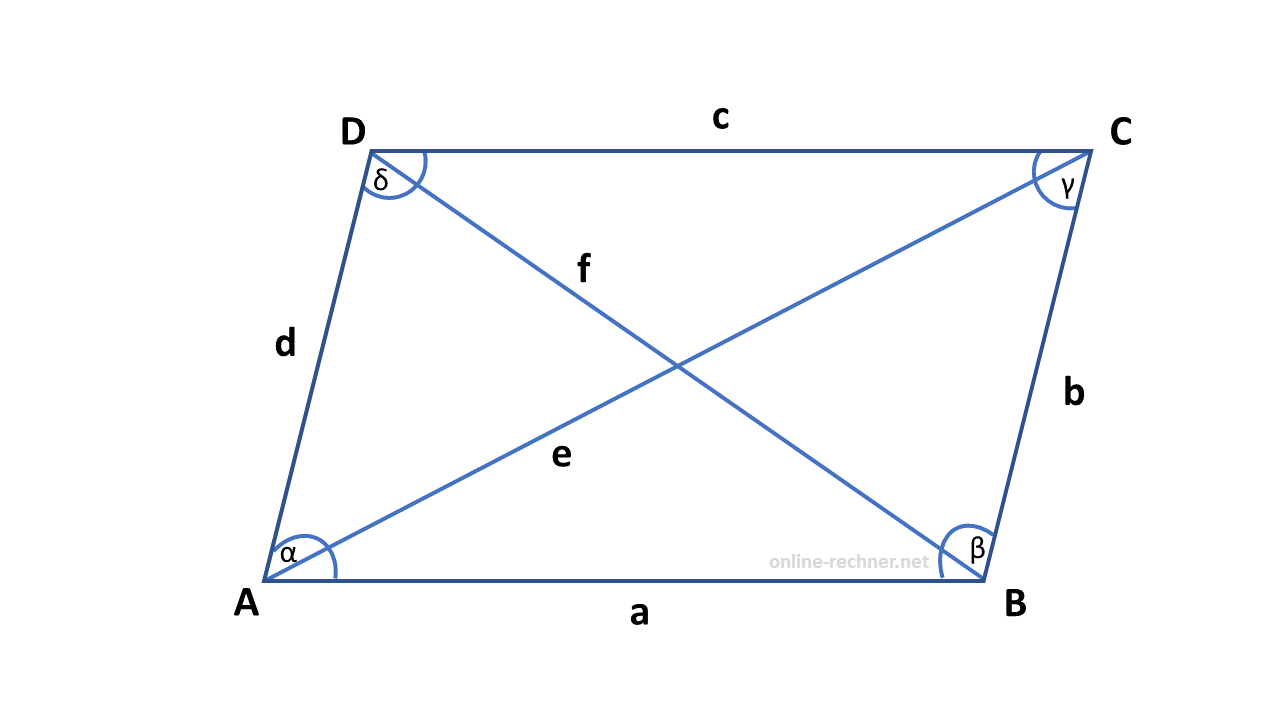
Flächeninhalt einer Raute
Formel: a * ha = A (Fläche)
Beispiel-Rechnung: 5cm * 7cm = 35cm2
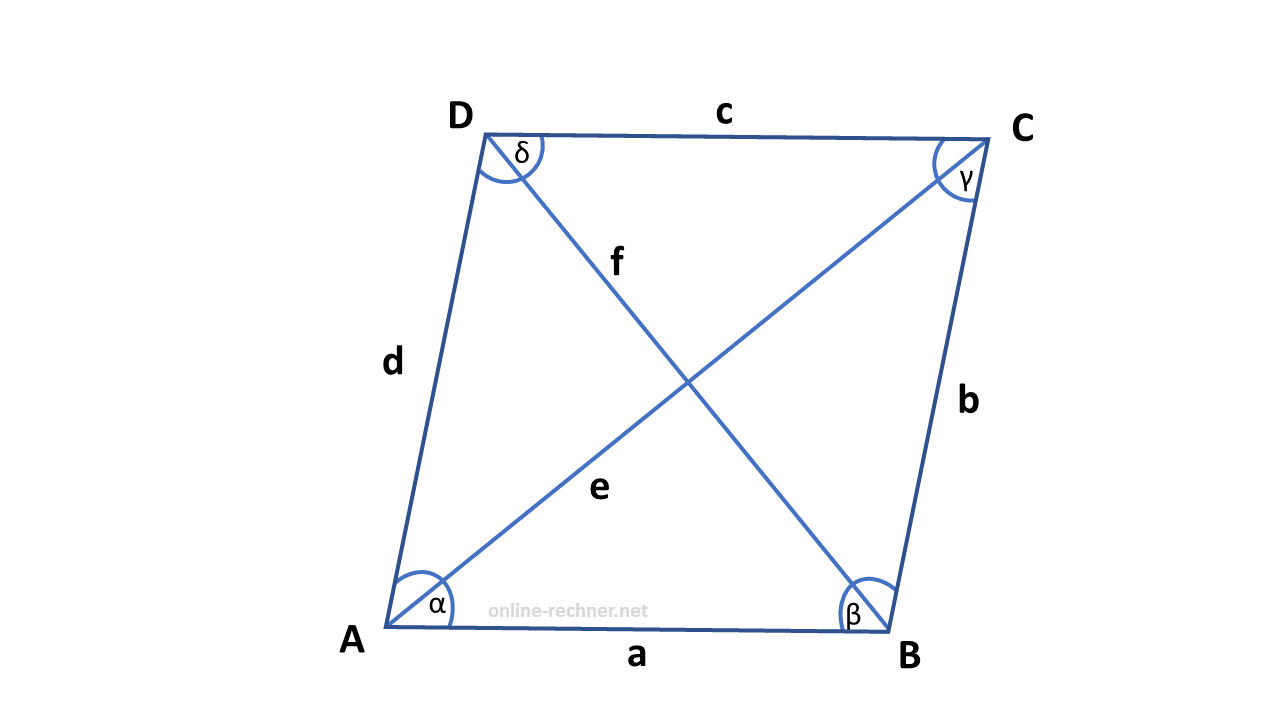
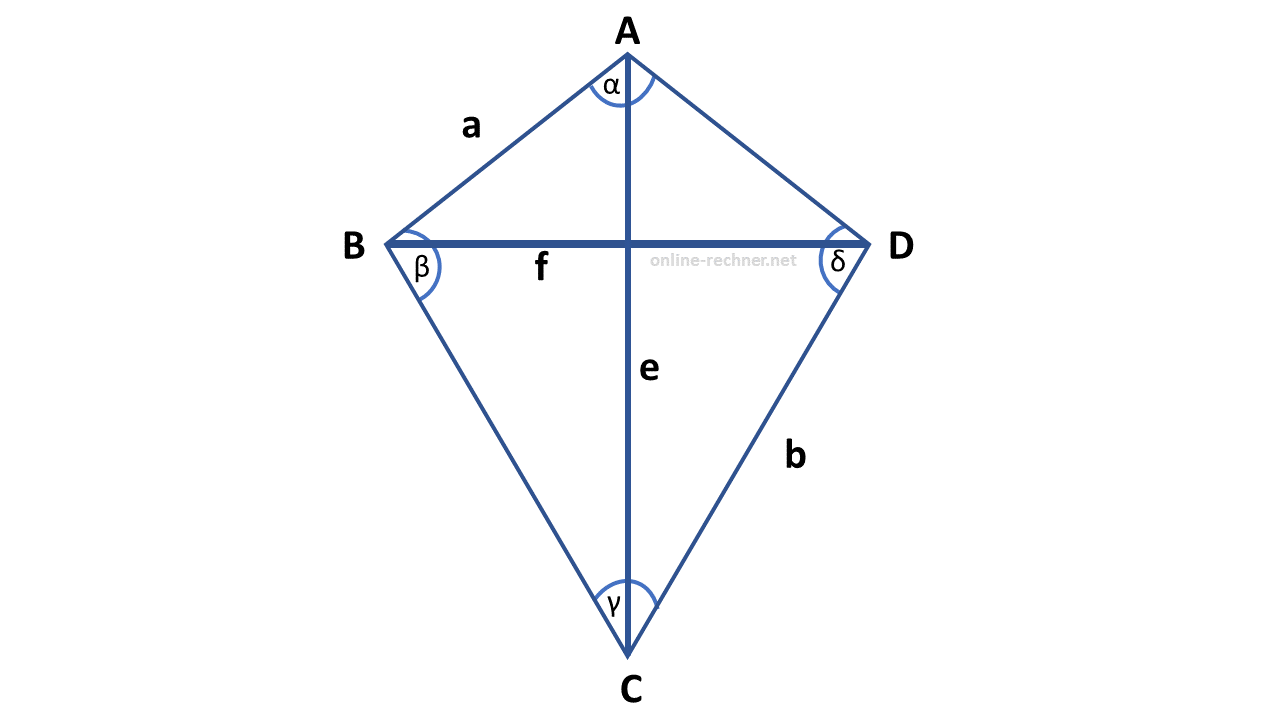
Flächeninhalt eines Deltoids
Formel: (e * f) / 2 = A (Fläche)
Beispiel-Rechnung: (3cm * 5cm) / 2 = 7,5cm2
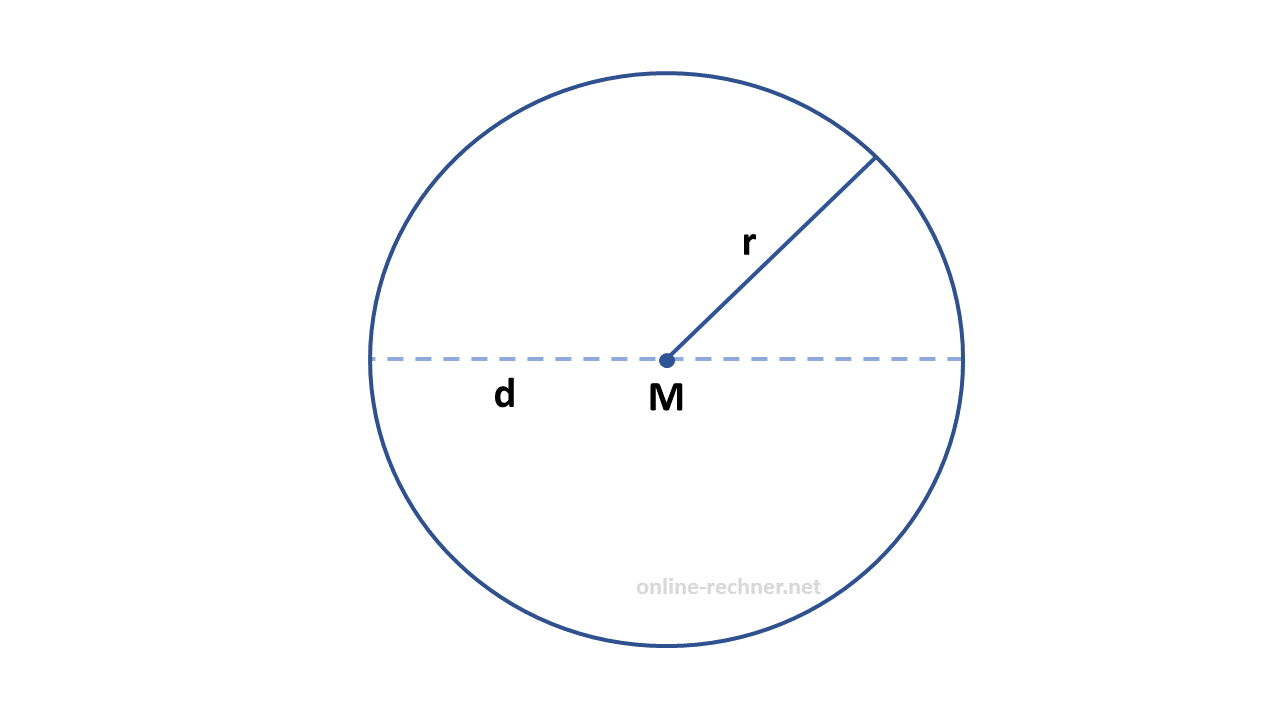
Flächeninhalt eines Kreises
Formel: Π * r2 = A (Fläche)
Π = 3,141592
Es werden für Pi hier nur 6 Dezimalstellen angezeigt.
Beispiel-Rechnung: Pi (Π) * 5cm2 = 78,54cm2
Die Berechnung des Flächeninhalts ist ein zentraler Aspekt in der Mathematik, insbesondere in der Geometrie. Der Flächeninhalt ist definiert als die Menge an Raum, die eine zweidimensionale Form oder Figur einnimmt. Die spezifische Formel zur Berechnung des Flächeninhalts variiert je nach Art der Figur.
1. Rechteck: Der Flächeninhalt eines Rechtecks wird berechnet, indem man die Länge mit der Breite multipliziert (A = Länge * Breite).
2. Quadrat: Da alle Seiten eines Quadrats gleich lang sind, kann der Flächeninhalt berechnet werden, indem man die Länge einer Seite quadriert (A = Seite²).
3. Kreis: Der Flächeninhalt eines Kreises wird berechnet, indem man das Quadrat des Radius mit Pi (ungefähr 3,14159) multipliziert (A = Pi * Radius²).
4. Dreieck: Der Flächeninhalt eines Dreiecks wird berechnet, indem man die Basis mit der Höhe multipliziert und dann durch 2 teilt (A = 0,5 * Basis * Höhe).
Diese Berechnungen sind grundlegend für viele mathematische, wissenschaftliche, technische und konstruktive Anwendungen. Es ist wichtig zu beachten, dass diese Formeln nur für flache, zweidimensionale Formen gelten. Für dreidimensionale Formen wie Zylinder, Würfel oder Pyramiden werden andere Formeln verwendet, um das Volumen zu berechnen.







