Online-Rechner
Volumen einer Pyramide
Formel: (G * h) / 3 = V
G = Grundfläche der Pyramide (a2)
Beispiel-Rechnung: (5cm2 * 10cm) / 3 = 83,33cm3
Das Volumen beträgt 83,33cm3.
Mantel einer Pyramide
Formel: 4 * (1/2 * a * ha) = M
Beispiel-Rechnung: 4 * (1/2 * 5cm * 12cm) = 120cm2
Der Mantel beträgt 120cm2.
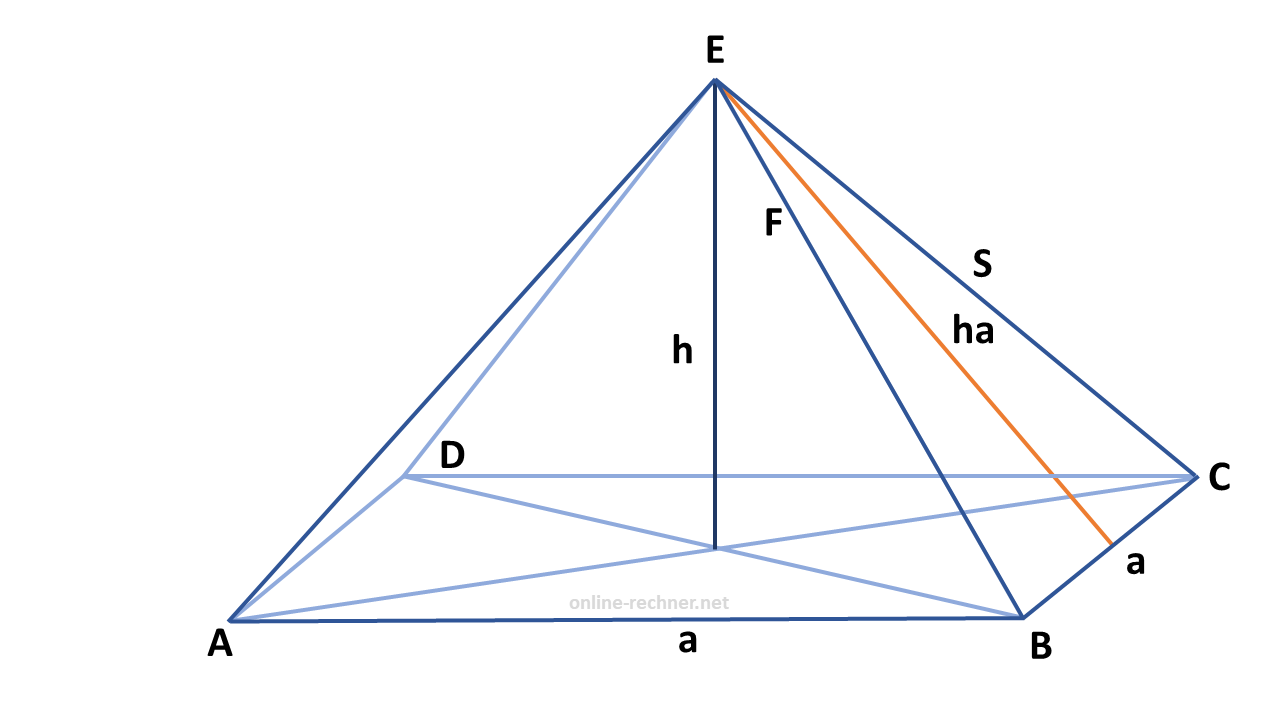
Oberfläche einer Pyramide
Formel: a2 + (4 * (1/2 * a * ha)) = O
Grundfläche = a2
Beispiel-Rechnung: 5cm2 + (4 * (1/2 * 5cm * 12cm)) = 145cm2
Die Oberfläche beträgt 145cm2.
Alle Angaben sind ohne Gewähr.
Eine Pyramide ist ein geometrischer Körper mit einer Grundfläche und einer vier-seitigen Mangelfläche. Die Formel zur Berechnung des Rauminhalts lautet: (G * h) / 3 = Volumen. Die Formel für die Mantelfläche lautet: 4 * (1/2 * a * ha) = M. Die Oberfläche wird mit der Formel a2 + (4 * (1/2 * a * ha)) = O berechnet.
Online-Rechner verwenden:
- Wählen Sie aus, ob Sie Volumen, Mantelfläche oder Oberfläche der Pyramide berechnen möchten.
- Geben Sie Ihre Angaben in den Rechner ein.
- Klicken Sie auf "berechnen", um Ihr Ergebnis zu erhalten.
Weitere Berechnungen:
Autor: Daniel Herndler
Auf dieser Webseite werden Berechnungen, Formeln und Beispielrechnungen mit einfacher Erklärung vom Autor online kostenlos bereitgestellt.