Skizze
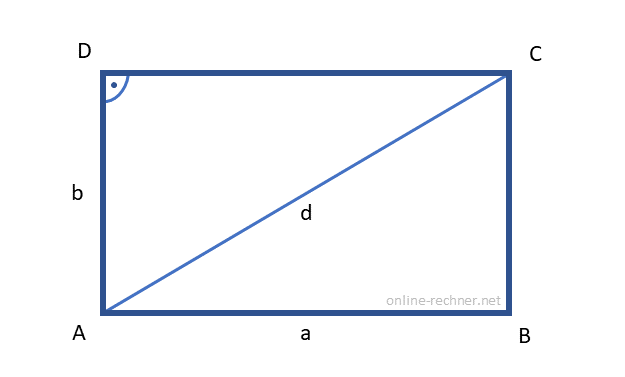
Umfang eines Rechtecks
Formel: 2a + 2b = U (Umfang)
Beispiel-Rechnung: (5cm * 2) + (3cm * 2) = 16cm
Fläche eines Rechtecks
Formel: a * b = A (Fläche)
Beispiel-Rechnung: 5cm * 3cm = 15cm2
Die Berechnung eines Rechtecks bezieht sich typischerweise auf das Finden seiner Fläche und seines Umfangs, gegeben seine Länge und Breite.
1. Fläche: Die Fläche eines Rechtecks berechnet sich durch Multiplikation seiner Länge mit seiner Breite. Die Formel lautet also: Fläche = Länge * Breite. Die Flächeneinheit ist typischerweise Quadratmeter (m^2), kann aber auch in anderen Quadratmaßeinheiten (wie Quadratzentimeter, Quadratkilometer usw.) ausgedrückt werden, abhängig von den gegebenen Maßeinheiten.
2. Umfang: Der Umfang eines Rechtecks wird berechnet, indem man die Längen aller Seiten zusammenzählt. Da ein Rechteck zwei gleich lange Seiten und zwei gleich breite Seiten hat, ist die Formel für den Umfang: Umfang = 2 * Länge + 2 * Breite. Der Umfang wird in der gleichen Maßeinheit wie Länge und Breite ausgedrückt, normalerweise in Metern, kann aber auch in Zentimetern, Kilometern usw. sein.
Zum Beispiel, wenn wir ein Rechteck mit einer Länge von 5 Metern und einer Breite von 3 Metern haben, wäre die Fläche 15 Quadratmeter (5m * 3m) und der Umfang 16 Meter (2*5m + 2*3m).
Diese einfachen Formeln sind grundlegend für viele Bereiche, von der Geometrie bis zur Architektur und Design. Es ist jedoch wichtig zu bedenken, dass sie nur für Rechtecke gelten, die rechte Winkel haben. Für andere Vierecke gelten andere Berechnungsmethoden.
